Matematyka dla medycyny

W niezbyt odległych czasach maturzysta, który miał bardzo dobre wyniki w nauce, ale niezbyt pewnie czuł się w obszarze matematyki (będącej kluczem do studiów technicznych, ekonomicznych oraz ścisłych) – często wybierał się na medycynę. Tam sukces zależał od wiedzy w zakresie biologii, chemii, nawet fizyki – ale nie matematyki.

Typowe medyczne zastosowania matematyki to statystyka. Za jej pomocą zmagamy się (skutecznie!) z trudnościami, jakie stawia przed nami niepowtarzalność i nieprzewidywalność zjawisk biologicznych.

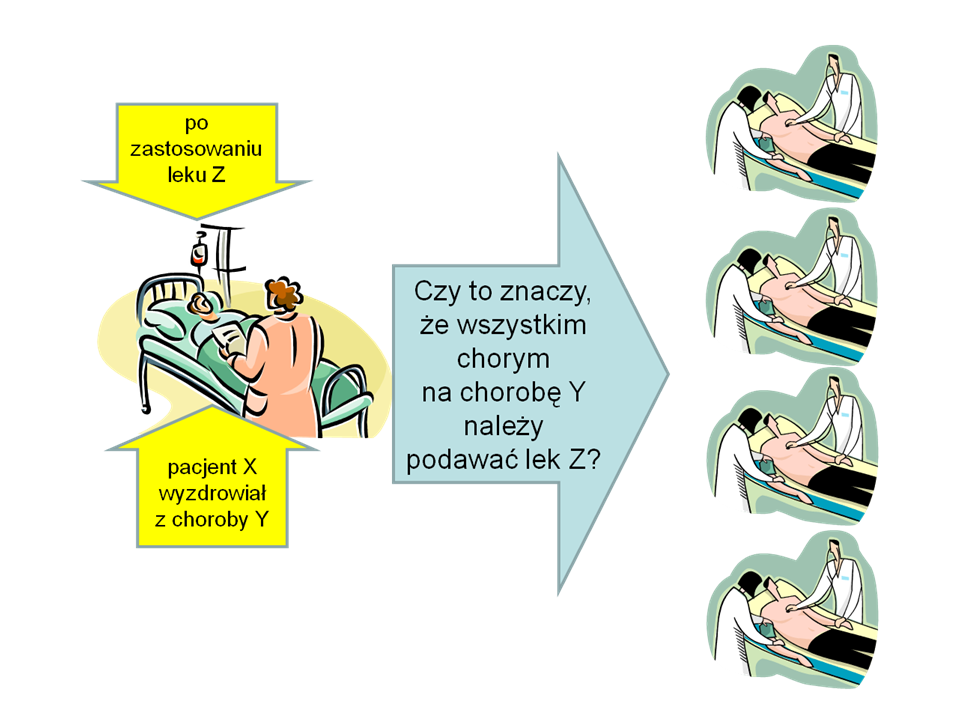
Każda pojedyncza obserwacja medyczna jest naukowo prawie bezwartościowa. Cóż z tego, że pacjent X wyzdrowiał z choroby Y po zastosowaniu leku Z? Mogło się przecież zdarzyć, że swoje wyzdrowienie pacjent X zawdzięczał własnej odporności, a zastosowane leczenie miało tu drugorzędne znaczenie. Mogło być tak, że choroba Y miała u pacjenta X nietypowy przebieg – na przykład była wywołana przez mniej zjadliwą odmianę wirusa. Mogło wreszcie być tak, że konkretna partia leku Z, który zażywał pacjent X, miała jakiś nietypowy przypadkowo dodany składnik, i to właśnie on uleczył pacjenta, a nie główny preparat stanowiący istotę leku Z. Wtedy inne partie leku Z, pozbawione tego dodatkowego składnika – okażą się nieskuteczne. No i wreszcie możliwe jest, że wyzdrowienie wywołał jakiś inny czynnik, o którym ani pacjent ani lekarz nie wiedzieli. Tak więc każda pojedyncza obserwacja medyczna jest obarczona licznymi czynnikami losowymi, jest niepewna.

Dla uzyskania pewności naukowej konieczne jest opierania wnioskowania na serii obserwacji. Dopiero wtedy, gdy określone zjawisko da się zaobserwować wielokrotnie w podobnej formie – można mówić o naukowo stwierdzonym fakcie.

Pojawia się jednak trudność. Jak wyciągać wnioski na podstawie zbioru obserwacji, skoro każda z nich jest trochę inna, indywidualna, niepowtarzalna?

Służy do tego statystyka.

Po pierwsze można z wielu obserwacji wyliczyć jeden wskaźnik, który te wszystkie obserwacje najlepiej reprezentuje. Można udowodnić, że jest on wolny od błędów, które obciążają każdą z rozważanych obserwacji z osobna. Taki wskaźnik nazywa się miarą tendencji centralnej. Może to być średnia, ale jest także mnóstwo innych możliwości (mediana, wartość modalna itp.). Te różne wskaźniki oferowane przez statystykę, mają różne zalety, więc się je starannie dobiera.

Po drugie można dokładnie odpowiedzieć na pytanie, jak dobrze użyta miara tendencji centralnej reprezentuje wszystkie rozważane dane. W tym celu ustalamy, jaka jest miara rozrzutu rzeczywistych danych wokół średniej. Ta miara (nazywana wariancją) pozwala ocenić, czy zaobserwowana różnica tendencji centralnych ma rzeczywistą wartość naukową, czy też jest wynikiem zbiegu okoliczności. Pojęcie wariancji najlepiej zilustrować na przykładzie. Oto obraz zbiorowości która jest bardzo rozproszona, w związku z czym wariancja jest tu duża:

A oto przykład zbiorowości, która jest skupiona, w związku z czym wariancja jest tu mała:

Wyobraźmy sobie, że po odkodowaniu informacji, kto był jak leczony i po przeliczeniu wyników okazało się, że pacjenci leczeni nową metodą mają średnio lepsze wyniki. Czy jest to już powód do świętowania sukcesu?
Niestety nie, bo trzeba najpierw zbadać wariancje w obu grupach.